Divisibilidad

Múltiplos y divisores

Si el cociente entre dos números, a:b, es exacto, diremos que "a es múltiplo de b" y se expresa así: a=b. También decimos que "b es divisor de a".

Por ejemplo, 30 es múltiplo de 5 porque 30:5 es un cociente exacto. Es decir, existe otro número, el 6, tal que 30= 5x6. El 5 es divisor de 30.

Propiedades de los Múltiplos y divisores

• Todo número natural es múltiplo de 1 y de sí mismo. Por ejemplo, 40 es múltiplo de 1 y múltiplo de sí mismo, pues 40= 1x40.

• Todo número natural tiene infinitos múltiplos. Por ejemplo, múltiplos de 12: 12, 24,36,48,...,120,132,..

• Cada número, a tiene al menos, dos divisores, 1 y a. Los restantes divisores de a forman parejas cuyo producto es a; salvo si a es cuadrado perfecto, en cuyo caso, uno de los divisores es raiz cuadrada de a, que se empareja consigo mismo.

• El 0 es múltiplo de cualquier número a, pues 0= ax0.

Números compuestos y Números primos

• Un  número compuesto es el que se puede expresar como producto de factores más simples. Por ejemplo, 12= 2x6.

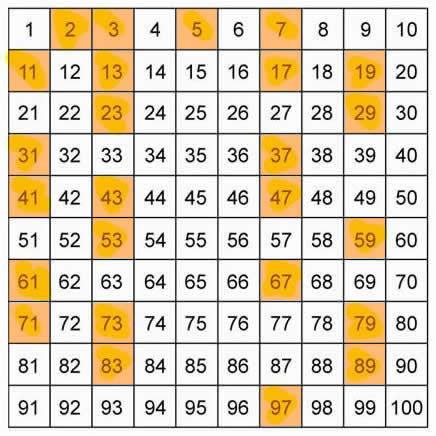
• Un número primo es el que no puede descomponerse en factores más simples. Estos son algunos números primos:

www.elestadomental.com

Criterios de divisibilidad

Para saber si un número es divisible por otro, basta efectuar la división y ver si es o no exacta. Sin embargo, resulta mucho más cómodo poseer criterios que nos permitan, con un solo golpe de vista o con un breve cálculo, saber si un número es divisible por otro. Algunos de estos criterios son:

www.aulacompartida.files.wordpress.com

Cómo averiguar si un número es primo o compuestos

Se comprueba que no es divisible por los sucesivos números primos hasta llegar a una división en la que el cociente sea menor o igual que el siguiente número primo. Si tampoco esta división es exacta, el número es primo.

Descomposición de un número en factores primos

Todo número compuesto se puede expresar como un producto de números primos. La obtención de los números primos cuyo producto da como resultado el número en  cuestión, se llama descomposición en factores primos o descomposición factorial.

www.librodigital.oupe.es

Máximo Común Divisor

Para hallar el Máximo Común Divisor de dos números se descomponen estos en factores primos y se toman los factores primos comunes elevados al menor exponente.

www.apuntesparaestudiar.com

Si el MCD de dos números es 1, se dice que son primos entre sí. Por ejemplo, 4 y 9 son primos entre sí.

Si a es múltiplo de b, el MCD (a,b) = b. Por Ejemplo MCD (60 y 15) = 15.

Mínimo Común Múltiplo 

Para hallar el m.c.m de dos números se descomponen estos en factores primos y se toman todos los factores que intervienen con el máximo exponente.

El m.c.m de dos números primos entre sí es su producto:

Si el MCD de (a,b) =1 entonces el m.c.m (a,b) = a·b

Si a es múltiplo de b, el m.c.m (a,b) = a

Ejercicios 

1. Comprueba si son primos; 223, 851, 227, 1073, 119, 2431.

2. ¿Cuál es la descomposición factorial de 90 · 660?

3. ¿Cuál es la descomposición factorial de 12 · 50 · 121 · 1144?

4. Escribe todos los divisores de 60

5. Escribe todos los divisores de 1050

6. ¿ Es a= 2^3 · 3 · 5^2 · 7 · 13 múltiplo de b= 2^3 · 3 · 5^2 · 13? ¿y de c = 2·5·11?

7. Considera a= 2^2 · 5·11 ; b = 2^2 · 11 ;  c) 22 · 3 · 52 · 11 ; ¿cuál es múltiplo de cuál?

Corrige tus Ejercicios pinchando aquí

Si quieres ejercicios de Divisibilidad ¡¡Pincha aquí!!