Sistemas de Ecuaciones

En las ecuaciones de dos incógnitas existen dos soluciones que hacen cierta igualdad. Una ecuación con dos incógnitas tiene infinitas soluciones. A estas incógnitas se les suele designar con las letras x e y aunque, sin embargo, pueden usarse otras letras. Algunos tipos de ecuaciones que nos podemos encontrar son:

Polinómicas:

• De primer grado Lineales: 2x - 5y = 7
• De segundo grado Cuadráticas: x^2 - y - 3 = 0
• De grado superior: x^2y - 3x + y^2 = 0

Radicales:

Representación Gráfica

Para obtener soluciones de una ecuación con dos incógnitas, se despeja una de ellas y se le dan valores a la otra:

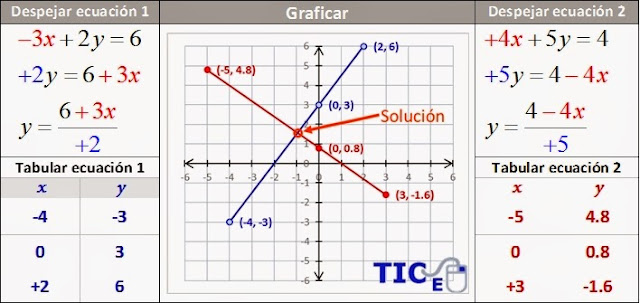
Si las soluciones de una ecuación lineal con dos incógnitas se interpretan como puntos del plano, entonces la ecuación se representa mediante una recta y sus soluciones son los puntos de esta.


Sistemas de Ecuaciones

Dos ecuaciones forman un sistema cuando lo que pretendemos de ellas es encontrar su solución común. Cuando dos ecuaciones forman un sistema, las ponemos de esta forma:

Se llama solución de un sistema de ecuaciones a la solución común entre ambas. A veces, en lugar de decir sistema de ecuaciones, diremos, simplemente sistema. Si ambas ecuaciones del sistema son lineales, las llamaremos lineales.

Los Sistemas Equivalentes

Dos sistemas son equivalentes cuando tienen la misma solución. Las rectas que representan a dos sistemas de ecuaciones equivalentes son distintas pero en ambos casos se cortan en el mismo punto (2,5) por ejemplo.

Número de Soluciones de un Sistema Lineal

En general, un sistema de dos ecuaciones lineales con dos incógnitas tiene una única solución. El punto donde se cortan las dos rectas, como ya hemos visto. Sin embargo, no siempre ocurre así:

• Sistema SIN solución: Esto ocurre cuando las dos ecuaciones dicen cosas contradictorias. Los sistemas que no tienen solución se llaman incompatibles. Gráficamente son dos rectas paralelas.

• Sistemas con INFINITAS soluciones: Los sistemas que tienen infinitas soluciones se llaman indeterminados. Gráficamente son dos rectas coincidentes: Todos sus puntos son comunes.

En qué consiste la resolución de un sistema

Consiste en modificar paso a paso el sistema inicial, de modo que cada nuevo sistema sea más sencillo que el precedente. En cada caso, el nuevo sistema ha de ser equivalente al anterior. Los métodos que nos permiten obtener, eficazmente, la solución de cualquier sistema lineal son:

• MÉTODO DE SUSTITUCIÓN: Consiste en despejar la incógnita en una de las ecuaciones y sustituir en la otra.

1. Se despeja una incógnita en una de las ecuaciones.
2. Se sustituye la expresión de esta incógnita en la otra ecuación, obteniendo una ecuación con una sola incógnita.
3. Se resuelve esta ecuación.
4. El valor obtenido se sustituye en la ecuación en la que aparecía la incógnita despejada. 
5. Se obtiene la solución.

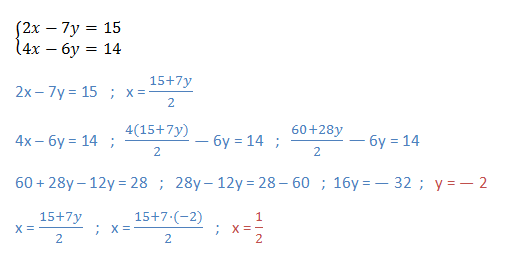
• MÉTODO DE IGUALACIÓN

Consiste en despejar la misma incógnita en ambas ecuaciones e igualar las expresiones resultantes.

1. Se despeja la misma incógnita en ambas ecuaciones.
2. Se igualan las expresiones, lo cual da lugar a una ecuación con una sola incógnita.
3. Resolvemos la ecuación resultante.
4. Sustituimos el valor de la y en cualquiera de las ecuaciones del paso primero.
5. Hacer comprobación.

• MÉTODO DE REDUCCIÓN

Este método consiste en preparar las dos ecuaciones para que una de las incógnitas tenga el mismo coeficiente en ambas.

1. Se preparan las dos ecuaciones (multiplicándolas por el número que convenga).
2. Al restarlas desaparece una de las incógnitas.
3. Se resuelve la ecuación restante.
4. El valor obtenido se sustituye en una de las iniciales y se resuelve.
5. Se tiene así la solución.

Ejercicios:

1. Representa las rectas correspondientes a estas ecuaciones. a) 2x-y = 3  b) -x+y = 1

2. Tenemos 53 Céntimos de euro repartidos en 16 monedas de dos céntimos y de 5 céntimos ¿Cuántas monedas de cada clase tenemos?

3. Tenemos 76 céntimos de euro en 20 monedas de 2 y de 5 céntimos. ¿Cuántas monedas de cada clase tenemos?

4. Representa los pares de sistemas y di si son equivalentes:

a) 3x -5y = 17
    2x + 4y =4

b) 3x - 5y = 0
    2x + 4y = 0

5. Fijándote bien en las ecuaciones que los forman, di cuál de los siguientes sistemas tiene una solución, cuál es incompatible y cuál indeterminado. Compruébalo representando las rectas.

a) x+y=5
    x+y=0

b) x+y=5
   -2x+5y=10

c) x+y=5
    2x+2y=10

d) x+y=5
    x-y=1

6. Completa los siguientes sistemas para que el primero tenga la solución x=5, y =3, el segundo sea incompatible y el tercero sea indeterminado y el cuarto también:

a) x - 4y = ___
   2x ___ = 13

b) 2x - y = 4
    4x + 2y = ___

c) 2x + y = 4
    4x+ ___= ___

d) 5x+ 11y = ___
    ___+ 33y = 9

7. Resuelve por el método de sustitución, los siguientes sistemas:

a) x+5y = 7
    3x-5y = 11

b) 5x + y = 8
    3x - 5y = 11

c) 3x + 10y= 6
    x+2y = 1

d) 5x - 3y = 50
    4x + y = 23

e) 3x+5y = 8
    3x + 4y = 1

8. Resuelve, por el método de igualación las siguientes ecuaciones:

a) x + 5y = 7
    3x-5y=11

b) 5x + y = 8
    3x - y = 11

c) 3x + 10y = 6
    x+2y = 1

d) 5x-3y=50
    4x + y = 23

9. Resuelve, por el método de reducción, los siguientes sistemas:

a) 3x + 5y = 11
    -4x - 5y = 38

b) 3x + 4y = 9
    5x + 2y = 15

c) x + 5y= 7
   3x - 5y = 11

d) 3x-5y = -26
   4x + 10y = 32

e) 5x - 3y = 50
    4x+y=234

10. Resuelve simplificando previamente:

a) 3(x-5)/2 - y-x/3 = y/6 + 3
    -3(x-y-4) - 10 = y-1

b) 2 (x-1) + 3(y+4) = 2 (3x+y) - 9
    x/2 - y/3 = 3

11. Resuelve este sistema aplicando dos veces el método de reducción:

45x - 11y =93
7x + 6y = 114

12. Dos poblaciones A y B distan 25Km. Un peatón sale de A hacia B a una velocidad de 4 Km/h. Un peatón sale de A hacia B a una velocidad de 4 Km/h. Simultáneamente, sale de B hacia A otro peatón a 6 Km/h. Calcula el tiempo que tardan en encontrarse y la distancia que ha recorrido cada uno hasta encontrarse.

13. Dos poblaciones están a 50Km. En el mismo instante salen un peatón de A hacia B a una velocidad de 5 K/h y un ciclista de B hacia A a 20 Km/h ¿Cuánto tardan en encontrarse? ¿qué distancia recorre el peatón?

14. La distancia entre dos ciudades, A y B, es de 300 Km. Un autobús sale de A hacia B a 105 Km/h. Calcula la distancia que recorre cada uno hasta el momento del encuentro.

15.  Completa los siguientes sistemas de ecuaciones para que ambos tengan la solución x=2, y =1:

a) 2x + 3y = ___
    3x - 4y  = ___

b) 3/2x + 7y= ___
    -2x - 5/2y = ___

16. Comprueba si x=-2, y= 1/2 es solución de los siguientes sistemas de ecuaciones:

a) 7x + 4y = -12
    3x - 2x = -7

b) x+2y= -3
    2x+6y =1

17. Resuelve por sustitución:

a) x= 2y +5
    3x - 2y = 19

b) y=5
    4x/3 + 2y/5 = 6

c) 5x - 4y =17
    6x-y = 9

d) 2x + 16 = 2y
    2y - 3x =16

18. Resuelve por igualación:

a) x = 2y/5
    x=4y-9

b) y=6x
    x= 2y-5/7

c) x+2y=5
    x-y=2

d)2y = 4x/3
   5y= 2x+2/3

e) 5+3y=2x
    x+2y=9

f) 7x-2y=8
    5x-3y=1

19. Resuelve por reducción:

a) x+y = 3
    x-y=9

b) 3x-5y= 9
    6x-2y=-6

c) 10x - 3y=1
    10x+3y=3

d) x-3y=21
    2x+5y=-35

20. Resuelve por el método que consideres más adecuado.

a) 3x = 6
5x - 4y/3 = 14

b) 6x - 3y = 5
    3x + 6y = 5

c) 5x + y = 6
    3x - 2y = 14

d) 1,2x + 0,7y= 7
    x- 0,5y = 1,5

e) 2y - x/3 = 1/15
    15x - 15y = 2

f) 5x= 2y -2
    4x = 20 - 2y

21. Resuelve los sistemas:

a) 3 (x-1) + 3 (y+4) = 2(3x+y) - 9
    x/2 - y/3 = 3

b) x+3/ y = 5
    2(x-3y) +x = 9

c) 3(x+2) -5 (y+1) = 9
    4x + 5+3y/2 = 5

d) 0,2x - 1,7y = 6,1
    1,23x + 0,8y = 3,75

22. Calcula dos números cuya suma sea 191 y su diferencia 67.

23. Dos kilos de peras y tres de manzanas cuestan 7,80€. Cinco kilos de peras y cuatro de manzanas cuestan 13,20€. ¿A cómo está el kilo de peras? ¿Y el de manzanas?

24. Para pagar un artículo que costaba 3€, he utilizado nueve monedas, unas de 20 céntimos y otras de 50 céntimos. ¿Cuántas monedas de cada clase ha usado?

25. Un fabricante de bombillas obtiene un beneficio de 0,3€ por cada pieza que sale del taller para la venta, pero sufre una pérdida de 0,4€ por cada pieza defectuosa que debe retirar. En una jornada ha fabricado 2100 bombillas obteniendo unos beneficios de 484,4€ ¿Cuántas bombillas válidas y cuántas defectuosas se han fabricado en ese día?

26. Una empresa aceitera ha envasado 3000 litros de aceite en 1200 botellas de dos y de cinco litros. ¿Cuántas botellas de cada una se han envasado?

27. En un bar se venden bocadillos de jamón a 3,5€ y bocadillos de tortilla a 2€. En una mañana vendieron 52 bocadillos y la recaudación final fue de 149€. ¿Cuántas se vendieron de cada clase?

28. En un test de 30 preguntas se obtienen 0,75 puntos por cada respuesta correcta y se restan 0,25 puntos por cada error. Si mi nota ha sido 10,5 ¿Cuántos aciertos y cuántos errores ha cometido?

29. Una empresa de productos plásticos recibe el encargo de fabricar cierto número de macetas para un día determinado. Al planificar la producción, el gerente advierte que si fabrican 250 macetas diarias, faltarían 150 macetas al concluir el plazo que se les ha dado. Si fabrican 260 macetas diarias, entonces sobrarían 80 macetas ¿Cuántos días de plazo tenían y cuántas macetas encargaron?

30.La base mayor de una trapecio es 2cm más larga que la menor; la altura del trapecio es 8cm y su área 48cm^2 ¿Cuánto miden las bases?

31. En una parcela rectangular de 44cm de perímetro se hace un jardín rectangular bordeado por un camino de 2m de ancho. Calcula las dimensiones de la parcela sabiendo que el área del jardín es de 45m^2.

32. María ha comprado un abrigo que estaba rebajado un 15%. Marta ha comprado otro abrigo 25€ más caro, pero ha conseguido una rebaja del 20%, con lo que sólo ha pagado 8 € más que María. ¿Cuál era el precio de cada abrigo?

33. Un capital, colocado en el banco durante un año, ha producido un beneficio de 800€. El beneficio habría sido el mismo si el capital hubiera aumentado en 2000€ y el interés anual se hubiera disminuido en un punto ( en un 1%) ¿A cuánto asciende el capital y a qué tanto por ciento ha estado colocado?

34. Por un pantalón y unos zapatos he pagado 126€. Si el precio del pantalón aumentara en un 14%, entonces sería el 75% del precio de los zapatos. ¿Cuánto pagué por cada uno?

35. He pagado 90,50€ por una camisa y un jersey que costaban, entre los dos, 110€. En la camisa me han rebajado un 20% y en el jersey un 15% ¿Cuál era el precio original de cada artículo?

36. En un centro escolar hay matriculados 795 estudiantes entre los dos cursos de Bachillerato. El 45% de primero y el 52% de segundo son mujeres, lo que supone un total de 384 alumnas entre los dos cursos. ¿Cuántos estudiantes hay en cada curso?

37. Dos comerciantes emprenden un negocio para cuya realización fue necesario invertir 100000€. A loa hora de repartir beneficios, el primero cobró 2160€ y el segundo 1440€ ¿Qué cantidad invirtió cada uno?

38. Tres socios han obtenido un beneficio de 12.900€ ¿Qué cantidad corresponde a cada uno si para inicial el negocio el primero aportó 2/3 de lo que aportó el segundo y este 5/6 de lo que aportó el tercero?

Problemas de Ecuaciones

1. Si a un número le restas 12, se reduce a su tercera parte. ¿Cuál es ese número?

2. Calcula tres números sabiendo que:

• El primero es 20 unidades menor que el segundo.
• El tercero es igual a la suma de los dos primeros. 
• Entre los tres suman 120.

3. La suma de tres números naturales consecutivos es igual al cuádruple del menor. ¿De qué número se trata?

4. Si al cuadrado de un número le quitas su doble, obtienes su quíntuplo. ¿Cuál es ese número?

5. La suma de un número par, el que le sigue y el anterior es 282. Halla esos números.

6. Por un videojuego, un cómic y un helado, Andrés ha pagado 14,30€. El videojuego es 5 veces más caro que el cómic, y este cuesta el doble que el helado ¿Cuál es el precio de cada artículo?

7. Me faltan 1,80€ para comprar mi revista de informática preferida. Si tuviera el doble de lo que tengo ahora, me sobrarían 2€. ¿Cuánto tengo? ¿Cuánto me cuesta la revista?

8. Con 12€ que tengo, podría ir dos días a la piscina, un día al cine y aún me sobrarían 4,5€. La entrada a la piscina cuesta 1,50€ menos que la del cine ¿Cuánto cuesta la del cine?

9, Antonio tiene 15 años, su hermano Roberto, 13, y su padre, 43. ¿Cuántos años han de transcurrir para que entre los dos hijos igualen la edad del padre?

10 . La suma de las edades de los cuatro miembros de una familia es 104 años. El padre tiene 6 años más que la madre, que tuvo a los dos hijos gemelos a los 27 años. ¿Qué edad tiene cada uno?

11. Un depósito está lleno el domingo. El lunes se vacían sus 2/3 partes, el martes se gastan 2/5 de lo que quedaba, y el miércoles, 300 litros. Si aún quedó 1,10 ¿Cuál es su capacidad?

12. En el mes de agosto, cierto embalse estaba a los 3/5 de su capacidad. En septiembre, no llovió y se gastó 1/5 del agua que tenía. En octubre se recuperaron 700 000m^3, quedando llenos en sus tres cuartas partes ¿Cuál es su capacidad?

13. Dos albañiles que trabajan asociados reciben 1400€ como pago de cierto trabajo. ¿Cuánto debe cobrar el primero si el segundo trabajó 2/5 partes que el otro?

14. Roberto y Andrés compran una camisa cada uno, ambas del mismo precio. Roberto consigue una rebaja del 12% mientras que Andrés solo consigue el 8%. Así uno paga 1,4€ más que el otro ¿Cuánto costaba cada camisa?

15. Si un número aumenta en un 10%, resulta 42 unidades mayor que si disminuye en un 5%. ¿Cuál es ese número?

16. Calcula el capital que, colocado al 8% durante dos años, se convierte en 2900€ (los intereses se suman al capital al final de cada año).

17. ¿Durante cuántos años se ha de colocar un capital de 2380€, con un interés anual del 3%, para conseguir un beneficio de 357€?

18. Un inversor pacta la compra de un terreno, valorado en 24000€, mediante dos pagos: el primero, de 12000€, a la firma de las escrituras, y el segundo, de 12300€, seis meses más tarde ¿Con qué interés se penaliza la demora?

19. Un inversor que dispone de 28000€, coloca parte de su capital en un barco al 8%, el resto, en otro banco, al 6%. Si la primera parte le produce anualmente 210€ más que la segunda, ¿Cuántos litros había en el bidón?

20. Se ha vertido un bidón de aceite de orujo, de 1,6€/L, en una tinaja que contenía 400 litros de aceite de oliva de 3,2 €/L. Sabiendo que el litro de la mezcla cuesta 2,60€/L ¿Cuántos litros había en el bidón?

21. ¿Cuántos litros de agua de grifo, a 15ºC, hay que añadir a una olla que contenía 6 litros de agua a 60ºC, para que la mezcla quede a 45ºC?

22. Mezclando 15Kg de arroz de 1€/Kg con 25Kg de arroz de otra clase, se obtiene una mezcla que sale a 1,30 €/Kg ¿Cuál será el precio de la segunda clase de arroz?

23. Se han mezclado 30 litros de aceite barato con 25 litros de aceite caro, resultando la mezcla a 3,20€/Kg. Calcula el precio del litro de cada clase, sabiendo que el de más calidad es el doble de caro que el otro.

24. Un ciclista que va a 18Km/h tarda 45m en alcanzar a otro que le lleva una ventaja de 6Km ¿Qué velocidad lleva el que va delante?

25. Un ciclista sale a la carretera a una velocidad de 15Km/h, ¿Qué velocidad deberá llevar el otro ciclista si sale media hora después y pretende alcanzar al primero en hora y media?

26. Un coche sale de una ciudad A, hacia otra B distante 315 Km, a una velocidad de 105 Km/h. Simultáneamente sale de B hacia A un camión que tarda en cruzarse con el coche una hora y 45min. ¿Cuál era la velocidad del camión?