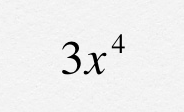Monomios

Un monomio es el producto indicado de un número por una o varias letras. En un monomio, la parte literal representa números de valor desconocido. Por eso conservan todas las propiedades de los números y sus operaciones.

El coeficiente es el número que interviene.

Se llama grado de un monomio al número de factores que forman su parte literal. Los números son monomios de grado cero, pues x^0 =1

Dos monomios son semejantes cuando tienen idéntica la parte literal.

• Valor Numérico de un Monomio

El valor numérico de un monomio para ciertos valores de las letras que intervienen es el resultado que se obtiene al efectuar las operaciones con los números que resultan de la sustitución.

• Suma de Monomios

La suma de monomios semejantes es otro monomio también semejante a ellos cuyo coeficiente es la suma de coeficientes. Si dos monomios no son semejantes, su suma no se puede simplificar y hay que dejarla indicada.

• Productos de Monomios

El producto de monomios es otro monomio cuyo coeficiente es el producto de los coeficientes, y su parte literal, el producto de las partes literales.

Ejercicios

1. ¿Cuál es el grado de cada uno de los siguientes monomios?

a) -2/7 ab^2c^3

b) -3xy^2

c) 4/3 x^2y^5z^2

2. Halla el valor numérico de los monomios siguientes para x=3, y=-2, z=5

a) -6x^2yz

b) 3x^2

c) 4xy^2

d) -5x^2y^2z^2

e) yz

f) -2xz^3

3. Efectúa las siguientes sumas de monomios:

a) 5x-3x+4x+7x-11x+x

b) 3x^2y-5x^2y + x^2y

c) 7x^3-11x^3+3y^3-y^3+2y^3

4. Escribe dos monomios semejantes a cada uno de los siguientes:

a) -5ab^2c^3

b) 11x^4

c) x

3. Expresa con un monomio:

a) El perímetro de esta figura:

b) El área de esta figura:

c) El volumen del cubo que se puede formar con esta figura:

4. Traduce a lenguaje algebraico, empleando una sola incógnita:

a) Los tres quintos de un número menos 1:

b) La suma de tres números consecutivos:

c) Un múltiplo de tres más su doble:

d) La suma de un número y su cuadrado:

e) El producto de un número por su siguiente:

5. Traduce al lenguaje algebraico, empleando dos incógnitas:

"La suma de las edades que tenían un padre y su hijo hace 6 años"

6. Traduce al lenguaje algebraico, utilizando dos incógnitas:

a) Un número más la mitad de otro.

b) El cuadrado de la suma de dos números.

c) La diferencia de los cuadrados de dos números.

d) El doble del producto de dos números.

e) La semisuma de dos números.

Lenguaje Algebráico

Trabajar en lenguaje algebraico consiste en manejar relaciones numéricas en las que una o más cantidades son desconocidas. 

Estas cantidades se llaman variables, incógnitas o indeterminadas y se representan con letras. Hay expresiones algebraicas de muy distinto tipo:

• Monomios

• Polinomios

Algunas expresiones algebraicas son igualdades:

• Identidades: La segunda parte de la igualdad se consigue operando en la primera.

• Ecuaciones: La igualdad sólo es cierta para algún valor de x. x= 5

Recuerda los formalismos Algebraicos

1. El factor 1 no se escribe.
2. El exponente 1 tampoco se escribe.
3. El divisor 1 no se pone.
4. El signo de multiplicación tampoco se pone.
5. El número de delante de la letra se rige por la propiedad conmutativa.
6. Se da la propiedad distributiva.

Diferencias

• Constante: Son letras cuyo valor nunca cambia.
• Variable: Son letras que pueden tomar cualquier valor entre un conjunto de valores.
• Incógnita:  Son las letras que sólo pueden tomar un determinado valor.

Ejercicios: 

1. Expresa mediante una ecuación las siguientes relaciones:

a) La edad de Ángel, dentro de 15 años, será el doble de la que entonces tenga Marisa.

b) Si gasto 2/5 de lo que tengo y además 60€, me quedaré con la mitad de lo que tenía al principio.

c) La Edad de Ángel dentro de 5 años será el cuadruplo de la que tiene ahora Marisa.

2. Asocia una expresión algebraica a cada uno de estos enunciados:

a) A un número le quitas 7

b) El doble de un número más su cuadrado

c) Un múltiplo de 3 menos 1

d) El 20% de un número

e) Cuatro veces un número menos sus dos tercios.

f) El precio de un pantalón aumentado en un 10%

g) Un número impar

3. Llama x al ancho de la pizarra y expresa su altura en cada caso:

a) La altura es la mitad del ancho

b) La altura es 20cm menos que el ancho

c) La altura es los 3/4 del ancho.

d) La altura es un 20% menos que su ancho

Calculo Mental

1. Calcula mentalmente:

a) 7-2+4

b)7 -(2-4)

c) 11+3x5-2

d)11+3x(5-2)

e)7-(2+4)

f)-7+2-4

g)(7+3)x5-2

h)(7+3) x (5-2)

2. Calcula mentalmente:

a) La cuarta parte de 100,200,600 y 1000

b) Los cuadrados de los números del 1 al 12

c) Los cubos de los números del 1 al 5

d) Las potencias de base 2 hasta 2^10

3. Calcula mentalmente el número decimal equivalente en cada fracción:

1/2; 3/4; 1/4; 1/5; 2/5; 3/5

4. Calcula mentalmente:

a) (-2)^5

b) (-2)^8

c) (-1)^10

d) (-1)^23

5. Calcula mentalmente

a) 20 x (-350)

 

b) 2 x 75x (-2)

c) 2486 x 50

d) 50x60 / 20

e) 1640 x 4

f) 120x25

6. Calcula

a) 2/3 de 60

b) 3/4 de 100

c) 3/500 de 500

d) La mitad de 2/3

e) La tercera parte de 12/7

f) La mitad de la quinta parte de -6

7. Calcula

a) Los 3/4 de un número valen 12. ¿Cuál es el número?

b) Los 2/3 de un número valen 20. ¿De qué número se trata?

c) Los 3/5 de una cantidad son 15. ¿Cuál es esa cantidad?

8. Calcula y simplifica

a) 3/5 x 2/3

b) 6 x 3/4

c) 5: 3/4

d) 1/3 x 4/5 

e) 8/3: 2/3

f) 2/7:4

9. Calcula

a) 1/2 + 1/4

b) 1/2 - 1/4

e) 1+ 1/3

c) 2- 1/4

d) 1+1/2

f) 1/2-1/3