Los números decimales sirven para expresar medidas, pues pueden designar valores intermedios entre los números enteros.
Un número decimal, tiene una parte entera y parte decimal. Los enteros pueden ser considerados como decimales con ninguna cifra decimal.
Los números decimales se representan sobre la recta numérica, de tal manera que con ellos podemos aproximarnos mucho (tanto como queramos) a cualquier punto de ella.
Siguiendo de este modo, el punto rojo puede designarse mediante un número decimal, con tanta aproximación como queramos.
Sin embargo, hay puntos de la recta que sólo se pueden describir con infinitas cifras decimales.
1.1 Operaciones
Los números decimales pueden operarse (suma, resta, multiplicación, división, potencia, raíz cuadrada...), y el resultado es, también, un número decimal.
Recordemos la jerarquía de operaciones y el uso de paréntesis:
- En las operaciones a · b - c y a + b : c. la multiplicación o la división tienen prioridad sobre la suma o la resta.
- La potencia tiene prioridad sobre cualquier operación.
- Si queremos romper esas prioridades tendremos que utilizar paréntesis.
2. Fracciones
Para medir, suele ser necesario fraccionar la unidad. De aquí surge la idea de número fraccionario: la mitad, la quinta parte, la milésima parte... de la unidad. Estos números se expresan numéricamente mediante fracciones.
Son números fraccionarios las fracciones anteriores. En todos ellos, el numerador es menor que el denominador, y por tanto, son partes de la unidad. Estas fracciones se llaman propias.
Si el numerador es mayor que el denominador, la fracción es mayor que la unidad, y se llama fracción impropia.
Si el numerador es múltiplo del denominador, la fracción no representa un número fraccionario, sino un número entero.
También las fracciones negativas representan números enteros o fraccionarios, según si el numerador es múltiplo o no del denominador.
El conjunto de todos los números enteros y todos los números fraccionarios se llama conjunto de números racionales y se designa con una Q. Los números racionales son, pues, los que se pueden poner en forma de fracción.
2.1 Simplificación de fracciones
Si el numerador y el denominador de una fracción se pueden dividir por un mismo número, al hacerlo, diremos que hemos simplificado o reducido la fracción. La nueva fracción que se obtiene es equivalente a la primera, pues ambas representan el mismo número racional.
Cuando una fracción no se puede reducir más porque numerador y denominador son primos entre sí, diremos que es irreducible.
Dos fracciones son equivalentes cuando se simplifican dando lugar a la misma fracción irreducible.
2.2 La fracción como operador
Cuando una fracción actúa como un operador de una cantidad, la cantidad resultante se obtiene multiplicando la cantidad por el numerador y dividiendo por el denominador, de esta manera:
2.3 Comparación de fracciones
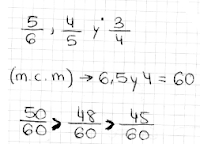 Si dos fracciones tienen distinto denominador, son difíciles de comparar. Por eso, para comparar fracciones, las reducimos a común denominador, es decir, buscamos fracciones respectivamente equivalentes a ellas que tengan el mismo denominador. Si las fracciones son irreducibles, este denominador debe ser múltiplo común de los denominadores de partida, preferiblemente el mínimo común múltiplo de ellos, así:
Si dos fracciones tienen distinto denominador, son difíciles de comparar. Por eso, para comparar fracciones, las reducimos a común denominador, es decir, buscamos fracciones respectivamente equivalentes a ellas que tengan el mismo denominador. Si las fracciones son irreducibles, este denominador debe ser múltiplo común de los denominadores de partida, preferiblemente el mínimo común múltiplo de ellos, así:
También se pueden comparar multiplicando en aspa las dos fracciones como en el siguiente ejemplo:
2.4 Representación en una recta
Los números fraccionarios pueden ser representados en la recta junto con los enteros:
De este modo, se tendrían todos los números racionales. Éstos se aglomeran en la recta de tal manera que, entre cada dos de ellos, hay otros infinitos. Pero, a pesar de ello, aún quedan infinitos puntos sin cubrir.
3. Operaciones con fracciones
3.1 Suma y resta de fracciones
Para sumar fracciones con el mismo denominador, se suman sus numeradores y se mantiene el denominador.
Para sumar fracciones con distinto denominador, tendremos que transformarlas en otras equivalentes con el mismo denominador. Reduciendo a común denominador, la suma de las fracciones se limita a la suma de sus numeradores (números enteros), las propiedades de la suma de números racionales son las mismas que las de la suma de enteros.
La resta se comporta como la suma. Basta con tener en cuenta los signos que actúan como en los números enteros.
3.2 Producto de fracciones
El producto de dos fracciones es otra fracción cuyo denominador es el producto de sus denominadores y cuyo numerador es el producto de sus numeradores.
3.3 Cociente de fracciones
El cociente de dos fracciones es el producto de la primera por la inversa de la segunda.
4. Potenciación
4.1 Potencia de exponente positivo
La potenciación, cuando el exponente es un número natural y, por tanto positivo, es muy fácil de interpretar.
Sus propiedades son sencillas de estudiar y de justificar:
5. Paso de fracción a decimal
Para obtener la expresión decimal de una fracción, se efectúa la división entre el numerador y el denominador. El cociente puede resultar:
- Número entero: 72/9 = 8
- Decimal exacto: 197/40 = 4,925
- Decimal periódico puro: 11/3 = 3,666...
- Decimal periódico mixto: 87/66 = 1,31818...
5.1 ¿Qué fracciones dan lugar a un decimal exacto o periódico?
Si la fracción es irreducible, se obtendrá un decimal exacto o un decimal periódico según como sea el denominador. Veamos los casos:
- Si el denominador solo tiene los factores primos 2 y 5, podemos transformarlo en una potencia de 10 multiplicándolo por el número adecuado. Por tanto, la fracción se podrá expresar como decimal exacto.
- Si el denominador tiene factores primos distintos de 2 y 5, la expresión decimal correspondiente no es exacta. Entonces, con seguridad, será periódica.
6. Paso de decimal a fracción
6.1 Decimal exacto a fracción
Expresar en forma de fracción un número decimal exacto es muy fácil. Basta con saber interpretarlo correctamente. Se coloca en el numerador el número decimal sin comas y en el denominador un 1 con tantos ceros como decimales tenía el número decimal. Ejemplo:
- 0,4 = 4/10
- 7,395 = 7395/1000
- 0.00814 = 814/100000
6.2 Decimal periódico a fracción
Pasar un decimal periódico a forma de fracción es menos fácil. Observa atentamente los siguientes ejemplos:
7. Números racionales
7.1 Las fracciones son números racionales
Una fracción a/b representa a:
- Un número entero, si el numerador es múltiplo del denominador.
- Un número fraccionario, si el numerador no es múltiplo del denominador.
7.2 Las fracciones son números racionales
También sabemos que tanto los números decimales exactos como los decimales periódicos se pueden poner en forma de fracción. Por tanto, son números racionales.
8. Números no racionales
8.1 Raíces
La nomenclatura de las raíces es la siguiente:
8.2 Propiedades de las raíces
8.3 Raíces no exactas y otros números no racionales
La raíz cuadrada de dos no es entera, evidentemente. Pero tampoco es racional. Es decir, su expresión decimal no es exacta ni periódica.
En general, si la raíz n-ésima de un número no es exacta, entonces tampoco es racional. Por ejemplo son no racionales la raíz cuadrada de cinco, la raíz cúbica de cuatro, la raíz quinta de mil...
Los números no racionales se llaman irracionales. Hay infinitos, y hace tiempo que conoces uno de ellos: el número π. Aunque al calcular con él lo valoramos en 3,14 o en 3,1416, estas son aproximaciones a su verdadero valor, que consta de infinitas cifras no periódicas: π = 3,141592654...
Hay números no racionales. Se llaman irracionales, y sus expresiones decimales requieren infinitas cifras no periódicas. Son irracionales: π , las raíces no exactas y otros infinitos números.
9. Expresión aproximada de números y cantidades
Cuando en la práctica usamos números para obtener resultados de la vida real, solo damos algunas de sus cifras decimales redondeando su expresión.
Si una persona nos dice que gana 1300 €, seguramente en su nómina figura una cantidad ligeramente distinta. por ejemplo 1 324,56 €.
Para comunicar su sueldo, esa persona ha redondeado la cantidad usando solamente dos cifras significativas. Los ceros solo sirven para completar la expresión.
Se llaman cifras significativas a aquellas con las que se expresa un número aproximado. Solo se deben utilizar aquellas cuya exactitud nos conste.
Los números sirven, en la práctica, para expresar medidas, y las medidas son, casi siempre, aproximadas. Por eso, cuando los números decimales se utilizan en problemas práctico, el número de cifras significativas debe ser adecuado a la precisión con que conocemos aquello que se expresa.
Con tres o cuatro cifras se afina mucho. Solo mediciones altamente científicas superan (con propiedad) cuatro cifras significativas.
Cuando damos una cantidad de forma aproximada, cometemos un error. El error absoluto es la diferencia entre la cantidad real y la aproximada. Si esta se ha obtenido mediante redondeo, el error absoluto es menor que la última cifra significativa utilizada.
Una medida es tanto más precisa cuantas más cifras significativas tenga la cantidad con que se expresa.
10. Notación Científica
Un número puesto en notación científica consta de:
- Una parte entera formada por una sola cifra (la de las unidades).
- El resto de las cifras significativas puestas como parte decimal.
- Una potencia de base 10, que da el orden de magnitud de un número.








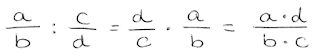









No hay comentarios:
Publicar un comentario
Nota: solo los miembros de este blog pueden publicar comentarios.